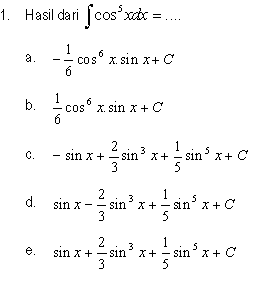Soal Latihan dan Pembahasan
Integral
Di susun Oleh :
Yuyun Somantri1
http://bimbinganbelajar.net/
Di dukung oleh :
Portal edukasi Gratis Indonesia
Open Knowledge and Education
http://oke.or.id
Tutorial ini diperbolehkan untuk di copy, di sebarluaskan, di print dan diperbaiki dengan tetap
menyertakan nama penulis、tanpa ada tujuan komersial
1 Lahir di Bandung tahun 1956, Lulus dari SMK Kimia melanjutkan studinya ke UPI (IKIP Bandung), lalu
meneruskan studinya lagi bidang matematika dan dari tahun 1984 sampai saat ini mengajar matematika di
SMA Negeri 3 Tasikmalaya
Integral
1. ò (3x2 - 4x + 5) dx = ....
Jawab :
x3 - 2x2 + 5x + c
2. ò = ÷
ø
ö ç
è
æ 3 + 1 + 6 dx .....
x
x
Jawab :
ò + + + = + + + = ÷ø
ö
çè æ
+ + - 3x x 6 dx 3. x 2x2 6x c 2x x 2 x 6x c
1
2
3
2
1
2
1
3 2
3. ò (3x - 1)(2x + 4) dx = .....
Jawab :
ò (6x2 + 10x - 4) dx = 2x3 + 5x2 - 4x + c
4. ò sin2 x cos x dx = ....
Jawab :
ò = + = +
= Þ =
u du u c x c
Misal u x du x dx
3
3
3 1
3
2 1 sin
sin cos
5. ò 2x sin x dx = .....
Jawab :
Diferensial Integral
2x Sin x
2 -cos x
0 -sin x
ò 2x sin x dx = - 2x cos x - (- 2sin x) + c = 2sin x - 2xcos x + c
1
6. ò ( - + ) =
2
0
3x2 3x 7 dx ....
Jawab :
[ 7 ] (8 6 14) (0 0 0) 16 2
0
2
2 3
x3 - x + x = - + - - + =
7. ò = ò = ò =
1
0
1
2
2
0
f (x) dx 2 dan 2 f (x) dx 2 maka f (x) dx .....
Jawab :
ò ò ò ò ò
ò ò
= + = - = - =
= Û =
2
0
1
0
2
1
1
0
1
2
1
2
1
2
( ) ( ) ( ) ( ) ( ) 2 1 1
2 ( ) 2 ( ) 1
f x dx f x dx f x dx f x dx f x dx
f x dx f x dx
8. Tentukan luas daerah yang dibatasi oleh garis y = 4x, sumbu X dan garis x = 5 !
Jawab : Y
5 X
= ò = [ ] =
5
0
5
0
L 4x dx 2x2 50
9. Tentukan luas daerah yang dibatasi oleh kurva y = - x2 + 2x dan sumbu X untuk 0 £ x £ 3
Jawab : Y
2 3 X
( ) ( ) [ ] [ ] 3
2 3
2
3 2
3
1
2
0
2
0
3 2
3
1
3
2
L = ò - x2 + 2x dx - ò - x2 + 2x dx = - x + x - - x + x = 2
2
10. Tentukan luas daerah yang dibatasi oleh kurva y = x2 - 6x dan sumbu X !
Jawab : Y
0 3 6
X
-9
Cara I : ( 6 ) [ 3 ] (72 108) 36 6
0
3 2
3
1
6
0
L = - ò x2 - x dx = - x - x = - - =
Cara II : y - y = 0 - (x2 - 6x) = - x2 + 6x Þ D = b2 - 4ac = 62 - 0 = 36 atas bawah
36
6.( 1)
36 36
6 2 2 =
-
= =
a
L D D
Cara III : .6.9 36 3
2
3 2
L = pl = =
11. Tentukan luas daerah yang dibatasi oleh kurva y = 6x - x2 dan y = x2 - 2x
Jawab :
3
64
6.( 2)
64 64
64 0 64
(6 ) ( 2 ) 2 8
2
2 2 2
2 1
=
-
=
= - =
- = - - - = - +
L
D
y y x x x x x x
12. Y Jika luas yang diarsir 32, maka tentukan ordinat
Puncak parabola !
X
4
Jawab :
32 .4 12 3
2
3 2
= Û =
=
y y
L pl
3
13. Tentukan isi benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = x3 , sumbu
X dan 0 £ x £ 2 diputar mengelilingi sumbu X sejauh 360 !
Jawab : Y
X
2
= ò = ò = [ ] =
2
0
2
0
7
7 1
6
2
0
3 2
7
V p (x ) dx p x dx p x 128p
14. Tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh parabola
y = x2 , y = 4x2 dan y = 4 diputar mengelilingi sumbu Y sejauh 360 !
Y
Jawab :
4
X
= ò - = ò - = ò = [ ] =
4
0
4
0
4
0
4
0
2
8
3
4 3
4
2 1
2
V p ( y )2 (1 y ) dy p y y dy p y dy p y 6p
15. ò x x dx = ......
Jawab :
ò x dx = x + c = x2 x + c
5
2
5 2
2
5
2
3
16. ò =
-
......
1 2
dx
x
x
Jawab :
ò = ò - = - + = - + = - - +
-
- = Þ - = Û = -
- dx u du u c u c x c
x
x
x u x dx du x dx du
2
2
1
2
1
2
2
2 1
. .2 1
1
1 2
2
1
2
1
4
17. ò =
+
......
2 3
12
2
dx
x
x
Jawab :
ò = ò = + = + +
+
+ = Þ = Û =
- dx u du u c x c
x
x
x u x dx du x dx du
.3 3.2 6 2 3
2 3
12
2 3 4 12 3
2
2
2
2
1
2
1
18. ò =
+
.....
2 8
18
3
2
dx
x
x
Jawab :
u du x c
x u x dx du
= + +
+ = Þ =
ò - .3 6 2 8
2 8 18 3
3
3 2
2
1
19. ò x ( x + 4)5 dx = ......
Jawab :
Diferensial Integral
x (x + 4)5
1 6
6
1 (x + 4)
0 7
42
1 (x + 4)
= x x + - x + + c = x - x + 6 + c
21
7 1
42
6 1
6
1 ( 4) ( 4) (3 2)( 4)
20. Jika f ‘(x) = 8x – 2 dan f(5) = 36 maka tentukan f(x) !
Jawab :
( )
( ) 4 2 54
(5) 4.5 2.5 36 54
( ) 8 2 4 2
2
2
2
= - -
= - + = Û = -
= ò - = - +
f x x x
f c c
f x x dx x x c
21. Diketahui f ‘(x) = (x+1)(x+2). Jika f(-3) = -3/2 maka tentukan f(x) !
Jawab :
( )
f x x x x
f c c
f x x x dx x x x c
( ) 2
( 3) 9 6 0
( ) 3 2 2
2
2 3
3
3
1
2 3
2
27
2
2 3
2
3
2 1
= + +
- = - + - + = - Û =
= ò + + = + + +
5
22. Diketahui = ax + b, f (0) - f (- 1) = 3 dan f (1) - f (0) = 5
dx
dF . Tentukan a+ b !
Jawab :
6
(1) (2) 2 4
(1) (0) 5 ( ) (0 0 ) 5 2 10 ...........(2)
(0) ( 1) 3 (0 0 ) ( ) 3 2 6 ........(1)
( ) ( )
2
2
2
2
+ =
= =
- = Þ + + - + + = Û + =
- - = Þ + + - - + = Û - + =
= ò + = + +
Maka a b
Dari dan didapat a dan b
f f b c c a b
f f c b c a b
f x ax b dx x bx c
a
a
a
23. ò sin (2x - 3) dx = .......
Jawab :
u du x c
x u dx du
= - - +
- = Þ =
ò sin . cos(2 3)
2 3
2
1
2
1
2
1
24. ò (x2 + 1)cos x dx = ......
Jawab :
Diferensial Integral
x2 + 1 cos x
2x sin x
2 -cos x
0 -sin x
( )
x x x x c
x x x x x c
= - + +
= + - - + - +
( 1)sin 2 cos
1 sin ( 2 cos ) ( 2sin )
2
2
25. ò (3x + 1) cos2x dx = ......
Jawab :
Diferensial Integral
3x+1 cos 2x
3 sin 2x 2
1
0 - cos2x 4
1
x x x c
x x x c
= + + +
= + - - +
(3 1)sin 2 cos2
(3 1)sin 2 ( cos2 )
4 3
2
1
4 3
2
1
6
26. ò sin3 x cos x dx = .......
Jawab :
ò = ò = +
= Þ =
x x dx u du x c
x u x dx du
4
4
sin3 cos 3 1 sin
sin cos
27. Tentukan nilai a yang memenuhi ò - = >
a
x dx dan a
1
(2 1) 6 0 !
Jawab :
ò - = Û [ - ] = Û - + = Þ =
a
a x dx x x a a a
1
1
(2 1) 6 2 6 ( 3)( 2) 0 3
28. Jika
20
( ) = x3 + x- 3 dan F(1) = - 11
dx
dF x maka tentukan ò
2
1
f (x) dx
Jawab :
( )
ò ò ( ) [ ]
ò
= - - = + - =
= - + = - Û = -
= + = - +
-
-
2
1
2
1
2
10 1
3
2
5 1
20
1
10
2 3
2
4 1
4
1
2
4
4
3 3 1
( ) 1
10
3
20
11
2
1
4
(1) 1
2
( ) 1
F x dx x x dx x x
F c c
c
x
F x x x dx x
x
29. Jika ( ) ò = ÷
ø
ö ç
è
= + + æ
2
1
2
3 3
3
1 4 dx .......
dx
y x maka dy x
Jawab :
( )
( )
ò ( ) [ ]
ò ò ò
= + = - =
+ = - + + = ÷
ø
ö ç
è
+ æ
- + = - = ÷
ø
ö ç
è
= + Þ = - Þ æ
-
- -
- - - -
2
1
2
1
3 1
3
2 2 1
2
1
2
1
2 2 2
2
1
4 4
2
2 2 2 4 4
2
3 1 2 2
3
1
6
17
4 4 2
2
x x x dx x
dx x x dx x x dx
dx
dy
x x x x
dx
x x dy
dx
y x x dy
7
30. Jika ò = ò - = >
a b
x dx x dx dan a b
0 0
3 2
2
1 , (2 3) 4 , 0
10
3 maka tentukan nilai a2 + 2ab + b2
Jawab :
[ ]
2 25
(2 3) 4 3 4 4
1
10
3
10
3
2 2
0
0
2
0
10
3
0
10
3
2
1 3
5
3
5
3
2
+ + =
- = Û - = Þ =
= Û = = úû
ù
êë é
= Û
ò
ò
a ab b
x dx x x b
x dx x a a
b
b
a a
31. Diketahui ò f (x) dx = ax2 + bx + c dan a ¹ 0. Jika a, f(a), 2b membentuk barisan aritmetika
dan f(b) = b maka tentukan nilai ò
1
0
f (x) dx
Jawab :
ò = ò + = [ + ] =
=
+
= + Þ + = + Þ = Þ =
- = -
+
= Þ + = Û =
= + Þ = +
1
0
1
0
2
4
1
1
0
2
1
4
4 1
2 1
2
4
( ) ( 4) 4 17
4
2. 1
2 ( ) 2 2(2 ) 2 6
( ) 2 ( )
, ( ),2 :
2 1
( ) 6 2 6 6
( ) 2 ( ) 2
f x dx x dx x x
f a a b a b a b a b
f a a b f a
a f a b barisan aritmetika maka
a
f b ab b b
f x ax b f a a b
32.
Jawab :
8

Soal No.1 Jawab :

Soal UN tahun 2005

Soal No.1 dapat diselesaikan dengan teknik Integral subtitusi, langkahnya :

- Ubah cos⁵x = cos⁴ x . cosx

= (cos²x)² .cosx = (1 – sin²x)².cosx

- Misalkan u = sin x , sehingga du = cosx.dx

- Jadi : ∫cos⁵x.dx = ∫(1 – sin²x)².cosx.dx

= ∫(1 – u²)² .du

= ∫(1 – 2u² + u⁴) .du

= u – 2/3u³ + 1/5u⁵

= sinx - 2/3sin³x+ 1/5sin⁵x + c

- Jawaban : D